Groove 3 just released a new video training series on Digital Performer 8 (MOTU), the new 64-bit version that now is available for the Mac and Windows, and it has a virtual festival of detailed information on MIDI, which spans several chapters . . .
Digital Performer 8 Explained by Eli Krantzberg (Groove 3 Inc.)MIDI tends to be like ReWire in the sense that the prevailing perspective is that everyone
automagically knows everything about it, hence user documentation is a bit beyond sparse, but so what . . .
I am optimistic regarding the ability of NOTION 4 (Notion Music) to work productively with DP8 for doing video scoring and sequencing, and this is one of the areas where DP8 clearly has advanced capabilities, which includes the ability to provide visual clues in a studio orchestra setting so that the various musicians see visual cues in addition to hearing the usual audio cues like click tracks, countdowns, and so forth . . .
DP8 has a special "Conductor" track, which is used in a similar way to the way NOTION handles real-time tempo adjustments, but the focus is a bit different, although the capabilities are similar . . .
I have not done a lot with Digital Performer for video scoring, but based on what I have read and observed, timing and sequencing is done very precisely, which is different from the way real-time tempo adjustments are done in NOTION . . .
Consider that there is a particular instant in a film or video where something dramatic happens and the orchestra needs to play a precisely timed "boom" or whatever . . .
In DP8 , the strategy is to mark this point in the film or video with a visual marker, which among other things provides precise timing information on the timeline or whatever, and this visual marker or cue then is used to determine exactly when stuff happens . . .
[
NOTE: It is easier to understand this stuff when you watch the video at the MOTU website for DP8 . . . ]
Digital Performer 8 Re-engineered Video Engine (MOTU)The "Conductor" track in DP8 has a tempo tapping feature, but it is different from the tempo tapping that NOTION does, where the focus in DP8 is on high precision timing and sequencing, which makes the way NOTION does tempo tapping ideal for live performances but
not so ideal for scoring to film and video. Conversely, the way Digital Performer does tempo tapping is
not ideally suited to live performances, where the preferred DP8 strategy is to provide a click track to which the live musicians and singers synchronize, which at best is awkward . . .
And while in many respects I have few if any actual clues about doing film and video scoring, I am conversant in what probably is the most practical way to make timing and sequencing adjustments the way these things are done in DP8, Logic Pro 9, and Final Cut Studio X, which is based on the way it was done over half a century ago using techniques from Joseph Schillinger's System of Musical Composition (SoMC), where there are specific techniques for adjusting music to fit precisely to film sequences or scenes, since in the SoMC the focus is similar in the sense of being intimately time-based, where as an example you have a scene scored at a specific tempo but the director decides to add 5 seconds of new material to the scene but simply adjusting the tempo will not work, which creates a bit of a dilemma that requires composing a few more measures of music but in a way that ensures it fits with the already composed music, thereby making it a combination of perhaps a tiny adjustment in tempo but more a matter of extending the theme in a mathematically and geometrically elegant way, where for example doing something like appending "Yeah! Yeah! Yeah!" to "Somewhere over the rainbow" is
not the brightest solution in the grand scheme of everything for extending a wonderful melody by a few seconds, where in this context the SoMC provides a virtual festival of different techniques, one of which will provide a few clues to a better strategy, where the focus is on introducing a bit of mathematics and geometry into the equation rather than on arbitrarily defining intuition . . .
The SoMC will
not make someone a skilled composer
automagically, but it does provide some insights and techniques which are especially useful for making adjustments to fit music to specific timelines, as shown in the simplified melody for "Over The Rainbow" (Harold Arlen and E. Y. Harburg) . . .
Somewhere Over The Rainbow ~ NOTION 3 Melody (Simplified)[
NOTE: In the following SoMC graphs, "p" is "pitch" and "t" is to "time", where the units of time are eighths. . . ]
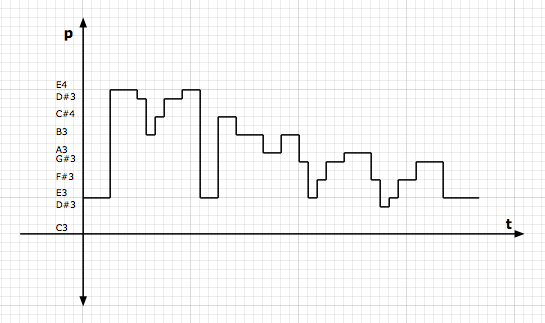Somewhere Over The Rainbow ~ SoMC Melody (Simplified)Both of these music notation systems provide the same information, but the SoMC version is more linear than logarithmic, which makes it easier to understand the various mathematical and geometrical aspects, where as shown in the following colorized version, there are repeating subpatterns . . .
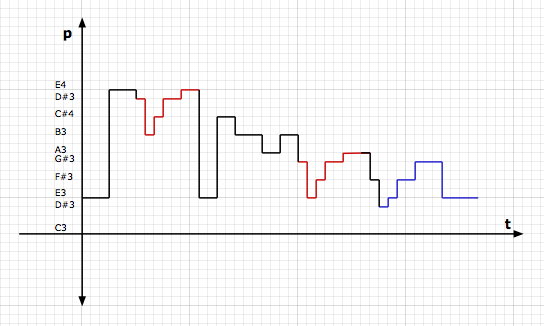Somewhere Over The Rainbow ~ SoMC Melody (Simplified) ~ Repeating Subpattern (Red, Blue)The red subpattern is easy to identify, but the subpattern also is shown in blue, except that the blue subpattern is flipped and stretched, as shown the following SoMC diagram, where the flipping is reversed (or normalized, if you prefer), with the primary focus being on the pitch intervals, but secondarily on the durations of the notes, of course . . .
[
NOTE: When I refer to "flipping", I am referring to a set of operations, where for example the high and low notes in the following two subpatterns are "flipped" horizontally. In other words, "flipping" refers to a set of transformations, which includes mirror imaging and other types of rotating, arranging, and so forth, where in this example the "flipping" is two-part, where it begins with a horizontal flip but then is followed with a vertical flip, while the durations of the high and low notes are flipped horizontally once the subpatterns are normalized, and the durations of the two middle notes are flipped vertically, which overall makes it two outer "flips" and two inner "flips", where these "flips" all are simple. And what you discover after a while is that when you include the complex flips, creating an elaborate melody requires only a few pitch intervals, where for example in this particular diatonic scale (Ionian), the pattern for the first four notes in the scale is the same as the pattern for the second four notes ([E, F#, G# A] = [B, C#, D#, E]), since in terms of half-steps both subpatterns are (2-2-2-1), which is a bit mind-boggling when you ponder it for a while, where it is important to understand that "flips" includes repeating a subpattern but at a vertical, horizontal, or angular offset . . . ]
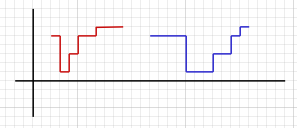Somewhere Over The Rainbow ~ SoMC Melody (Simplified) ~ Repeating Subpatterns (Normalized)The subpattern aspect might be easier to understand when you focus on the pitch intervals without respect to time, where the overall pattern is {1-8-7-5-6-7-8-1-6-5-4-5-3-1-2-3-4-2-0-1-2-3-1}, although perhaps not . . .
For me, it is easier to make sense of the SoMC graphs, since the patterns are represented visually, but once you understand the patterns geometrically, working with the integer numbers in an algebraic way is natural . . .
Traditional music theory has a virtual festival of ways to analyze and to explain this stuff, but none of it is mathematical in an absolute sense, and what happens is that you find yourself relying on arbitrary "rules" that are based on fitting hypotheses to facts, where the problem is that the hypotheses are arbitrary rather than absolute in the sense that music theorists correctly observe that certain patterns consistently work but never realize the mathematical and geometric reasons
why the patterns consistently work . . .
Using a surreal cooking analogy, metaphor, or simile, music theorists correctly observe that dill pickle slices taste good with hamburgers and ham sandwiches, and then have a team meeting where they decide that the "rule" should be that when one is making hamburgers and ham sandwiches it is good to include dill pickle slices, which is
spanky except that it does
not explain precisely
why dill pickle slices taste good with hamburgers and ham sandwiches, where the fact of the matter is that understanding
why this is the case requires one to switch to physiology, chemistry, the perceptions of taste, smell, and touch, as well as including a bit of
yin and
yang metaphysics, which is fabulous . . .
Fabulous! 
P. S. Regarding the "Yeah! Yeah! Yeah!" reference, one might suggest reasonably that "She Loves You" (John Lennon and Paul McCartney) is a variation of "Over The Rainbow" ((Harold Arlen and E. Y. Harburg) , really . . .
"Over The Rainbow" (Judy Garland) -- 1955 -- YouTube music video"She Loves You" (Beatles) -- 45 RPM Record -- YouTube music videoReally! 
